Question

1. Find the real or imaginary solutions for the following equation by factoring.125x3 - 27 = 0

Answer 1

The equation is given to be:

`125x^3-27=0`

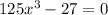
Applying the exponent rules, we have:

`\Rightarrow(5x)^3-3^3=0`

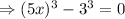
Recall the Difference of Cubes formula given to be:

`x^3-y^3=\mleft(x-y\mright)\mleft(x^2+xy+y^2\mright)`

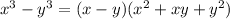
Therefore, the equation becomes:

`\begin{gathered} (5x-3)(\lbrack5x\rbrack^2+\lbrack3*5x\rbrack+3^2)=0 \\ (5x-3)(25x^2+15x+9)=0 \end{gathered}`

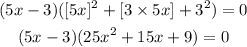
Using the Zero Factor Principle, we have that:

`\begin{gathered} (x-a)(x-b)=0 \\ \text{then} \\ x-a=0 \\ \text{and} \\ x-b=0 \end{gathered}`

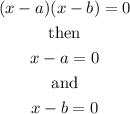
Therefore, we can have:

`\begin{gathered} 5x-3=0 \\ 5x=3 \\ x=(3)/(5) \end{gathered}`

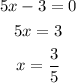
and

`25x^2+15x+9=0`

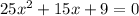
Solving the equation using the Quadratic Formula:

`x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

From the Quadratic Equation, we have:

`\begin{gathered} a=25 \\ b=15 \\ c=9 \end{gathered}`

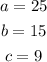
Therefore, we have:

`x=\frac{-15\pm\sqrt[]{15^2-\lbrack4*25*9\rbrack}}{2*25}=\frac{-15\pm\sqrt[]{225-900}}{50}=\frac{-15\pm\sqrt[]{-675}}{50}`

Recall that:

`\sqrt[]{-1}=i`

Therefore, we have that:

`x=\frac{-15\pm\sqrt[]{-1*675}}{50}=\frac{-15\pm i\sqrt[]{225*3}}{50}=\frac{-15\pm15i\sqrt[]{3}}{50}`

Hence, the values of x can be:

`x=\frac{-15_{}+15i\sqrt[]{3}}{50}=\frac{5(-3+3i\sqrt[]{3})}{50}=\frac{-3+3i\sqrt[]{3}}{10}=-(3)/(10)+i\frac{3\sqrt[]{3}}{10}`

or

`x=\frac{-15_{}-15i\sqrt[]{3}}{50}=\frac{5(-3-3i\sqrt[]{3})}{50}=\frac{-3-3i\sqrt[]{3}}{10}=-(3)/(10)-i\frac{3\sqrt[]{3}}{10}`

ANSWER:

`\begin{gathered} x=(3)/(5) \\ x=-(3)/(10)+i\frac{3\sqrt[]{3}}{10} \\ x=-(3)/(10)-i\frac{3\sqrt[]{3}}{10} \end{gathered}`