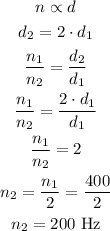Question

A. guitar string vibrates at 400 Hz and has a length of 0.8 m. Find the new frequency ifa) the string is lengthened to 0.9 m.b) the string is replaced with another string, the density of which is greater by a factor of two.c) the tension in the string is decreased by a factor of 0.4.d) the string is replaced with another string, the diameter of which is twice as large.

Answer 1

(a) 355.56 Hz

(b) 282.84 Hz

(c) 309.84 Hz

(d) 200 Hz

Explanation:

Given:

n1 = primary frequency = 400 Hz

L1 = primary length = 0.8 m

(a)

New length = L2 = 0.9 m

Frequency of the length is string isproportional to the length of the string. i.e n ∝ L1​

`\begin{gathered} (n_1)/(n_2)=(L_2)/(L_1) \\ n_2=(L_1\cdot n_1)/(L_2) \\ n_2=(0.8\cdot400)/(0.9) \\ n_2=355.56\text{ Hz} \end{gathered}`

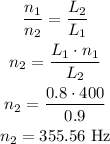
(b)

ρ is the density

`\begin{gathered} n\propto(1)/(√(\rho)) \\ \rho_2=2\rho_1 \\ (n_1)/(n_2)=\sqrt{(\rho_2)/(\rho_1)} \\ (n_1)/(n_2)=\sqrt[]{(2\rho_1)/(\rho_1)} \\ (n_1)/(n_2)=\sqrt[]{2} \\ n_2=\frac{n_1}{\sqrt[]{2}}=\frac{400}{\sqrt[]{2}} \\ n_2=282.84\text{ Hz} \end{gathered}`

(c)

T is the tension

`\begin{gathered} n\propto\sqrt[]{T} \\ T_2=T_1-0.4\cdot T_1 \\ T_2=0.6\cdot T_1 \\ (n_2)/(n_1)=\sqrt[]{\frac{T_2}{T_1_{}}} \\ (n_2)/(n_1)=\sqrt[]{(0.6\cdot T_1)/(T_1)} \\ (n_2)/(n_1)=\sqrt[]{0.6} \\ n_2=400\cdot\sqrt[]{0.6} \\ n_2=309.84\text{ Hz} \end{gathered}`

(d)

d is the diameter

`\begin{gathered} n\propto d \\ d_2=2\cdot d_1 \\ (n_1)/(n_2)=(d_2)/(d_1) \\ (n_1)/(n_2)=(2\cdot d_1)/(d_1) \\ (n_1)/(n_2)=2 \\ n_2=(n_1)/(2)=(400)/(2) \\ n_2=200\text{ Hz} \end{gathered}`