Question

A factory produces cars that are safe 80% of the time and uses a machine to test whether each car is safe. The machine marks safe cars incorrectly 10% of the time and unsafe cars incorrectly 40% of the time. If a car is marked as safe by the machine, what is the probability that it is actually unsafe?

Answer 1

0.5

Explanation:

Given:

• P(Safe), P(S)=80%=0.8

,

• P(Unsafe), P(U) = 1-0.8=0.2

,

• P(Marked Incorrectly | Safe)=P(I|S)=10%=0.1

,

• P(Marked Incorrectly | Unsafe)=P(I|U)=40%=0.4

We want to find the probability that a car is marked incorrectly (safe) given that it is actually unsafe.

By Baye's formula for conditional probability:

`\begin{gathered} P(Unsafe|Marked\text{ Incorrectly\rparen}=(P(I|U)P(U))/(P(I|U)P(U)+P(I|S)P(S)) \\ =(0.4*0.2)/(0.4*0.2+0.1*0.8) \\ =(0.08)/(0.08+0.08) \\ =(0.08)/(0.16) \\ =0.5 \end{gathered}`

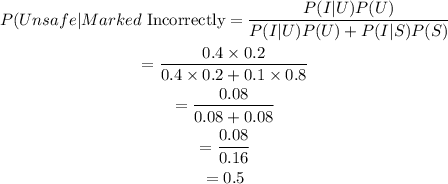
The probability that a car marked as safe is actually unsafe is 0.5 (or 50%).