Answer:
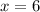
Step-by-step explanation:
To solve this, we need to use two properties of logarithms.
The first one is the difference of logarithms with same base:
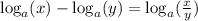
The second one is the definition of logarithm:
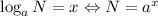
Then, we are given the equation:

Then:
![\operatorname{\log}_3(2x+1)-\operatorname{\log}_3(6x-23)=0]()
Applying the first property, for difference of logs:
![\operatorname{\log}_3((2x+1)/(6x-23))=0]()
Now we apply the definition of log:
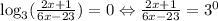
And now we can solve as any rational equation:
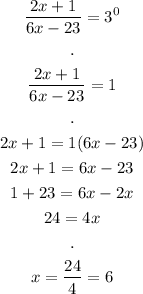
Thus, the answer is x = 6