Question

What is the distance between the point (3.6) and the midpoint of the line segment connecting (5. 6) and (7.-2)?

Answer 1

First, find the midpoint between (5, 6) and (7, -2)

Next, name the coordinates

x1 = 5

y1 = 6

x2 = 7

y2 = -2

Use the formula to find the mid-point of the line joining (5 , 6) and (7 , -2)

`\begin{gathered} \text{Mid}-p\text{oint = (}\frac{x_{1\text{ }}+x_2}{2}\text{ , }(y_1+y_2)/(2)) \\ =(\frac{5\text{ + 7}}{2},\text{ }\frac{6\text{ - 2}}{2}\text{ )} \\ =\text{ (}(12)/(2),\text{ }(4)/(2)\text{ )} \\ =\text{ ( 6,2)} \end{gathered}`

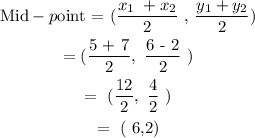
Mid-point of the line joining (5 , 6) and (7 , -2) = ( 6, 2 )

Next step, you find the distance between ( 3, 6) and ( 6, 2 )

Name the coordinates and write out the formula.

x1 = 3

y1 = 6

x2 = 6

y2 = 2

`\begin{gathered} \text{Distance betw}e\text{en two point = }\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ =\text{ }\sqrt[]{(6-3)^2+(2-6)^2} \\ =\text{ }\sqrt[]{3^2+(-4)^2} \\ =\text{ }\sqrt[]{9\text{ + 16}} \\ =\text{ }\sqrt[]{25} \\ =\text{ 5} \end{gathered}`

Final answer

Distance = 5 units