First, find the midpoint between (5, 6) and (7, -2)
Next, name the coordinates
x1 = 5
y1 = 6
x2 = 7
y2 = -2
Use the formula to find the mid-point of the line joining (5 , 6) and (7 , -2)
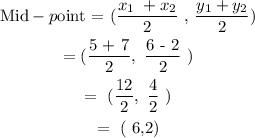
Mid-point of the line joining (5 , 6) and (7 , -2) = ( 6, 2 )
Next step, you find the distance between ( 3, 6) and ( 6, 2 )
Name the coordinates and write out the formula.
x1 = 3
y1 = 6
x2 = 6
y2 = 2
![\begin{gathered} \text{Distance betw}e\text{en two point = }\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ =\text{ }\sqrt[]{(6-3)^2+(2-6)^2} \\ =\text{ }\sqrt[]{3^2+(-4)^2} \\ =\text{ }\sqrt[]{9\text{ + 16}} \\ =\text{ }\sqrt[]{25} \\ =\text{ 5} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/tgwiqu5nlgm0vmml9iiddamz226kqkzxkp.png)
Final answer
Distance = 5 units