Question

A set of 4 consecutive even integers sums to -252. What is the value of the greatest integer?

Answer 1

Let us assume that the first even number is x

Then the first consecutive even is x + 2

The second consecutive even is x + 4

The third consecutive even is x + 6

The four consecutive even numbers are

x, x + 2, x + 4, x + 6

Their sum is -252, then

Add them and equate the sum by -252

`x+x+2+x+4+x+6=-252`

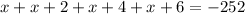
Add the like terms on the left side

`\begin{gathered} (x+x+x+x)+(2+4+6)=-252 \\ 4x+12=-252 \end{gathered}`

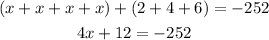
Now let us solve the equation

Subtract 12 from both sides

`\begin{gathered} 4x+12-12=-252-12 \\ 4x=-264 \end{gathered}`

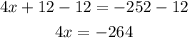
Divide both sides by 4 to find x

`\begin{gathered} (4x)/(4)=(-264)/(4) \\ x=-66 \end{gathered}`

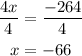
That means, the first even number is -66

-66 + 2 = -64

-66 + 4 = -62

-66 + 6 = -60

The four consecutive even numbers are

-66, -64, -62, -60

Let us find their sum to check the answer

-66 + -64 + -62 + -60 = -252

Then the answer is right

The greatest integer is -60