Question

Triangle A(-1.-3) B(-2,-2) C(1,4) is reflected over the x-axis and then rotated90 degrees counterclockwise. What are the coordinates of A"B"C"?

Answer 1

Step 1. Reflect each point over the x-axis.

To make an x-axis reflection, we use the following rule:

`(x,y)\longrightarrow(x,-y)`

Applying this to points A, B, and C, where A', B' and C' are the points after the reflection:

`\begin{gathered} A(-1,-3)\longrightarrow A^(\prime)(-1,3) \\ B(-2,-2)\longrightarrow B^(\prime)(-2,2) \\ C(1,4)\longrightarrow C^(\prime)(1,-4) \end{gathered}`

Step 2. Rotate the points 90° counterclockwise.

To make a 90° counterclockwise rotation we use the following rule:

`(x,y)\longrightarrow(-y,x)`

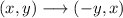
Applying this to the points A', B', and C', where A'', B'', and C'' will be the points after the rotation:

`A^(\prime)(-1,3)\longrightarrow A^(\doubleprime)(-3,-1)`

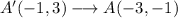
As we can see, after the rotation, the new x coordinate is the old y coordinate but with the opposite sign, and the new y coordinate is the old x coordinate.

We do the same for B', and C':

`\begin{gathered} B^(\prime)(-2,2)\longrightarrow B^(\doubleprime)(-2,-2) \\ C^(\prime)(1,-4)\longrightarrow(4,1) \end{gathered}`

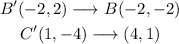
Answer:

A''(-3,-1), B''(-2,-2), C''(4,1)