Step 1. Reflect each point over the x-axis.
To make an x-axis reflection, we use the following rule:
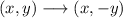
Applying this to points A, B, and C, where A', B' and C' are the points after the reflection:
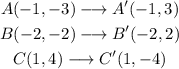
Step 2. Rotate the points 90° counterclockwise.
To make a 90° counterclockwise rotation we use the following rule:
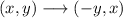
Applying this to the points A', B', and C', where A'', B'', and C'' will be the points after the rotation:
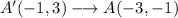
As we can see, after the rotation, the new x coordinate is the old y coordinate but with the opposite sign, and the new y coordinate is the old x coordinate.
We do the same for B', and C':
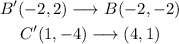
Answer:
A''(-3,-1), B''(-2,-2), C''(4,1)