Step-by-step explanationWe can find the area of the rectangle and then subtract the area of the semicircles to find the area of the paper that remains. Both semicircles form a circle. Then, we have:
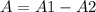
Finding the area of the rectangle
The formula to find the area of a rectangle is:
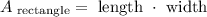
Then, we have:
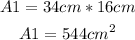
Finding the area of the circle
The formula to find the area of a circle is:
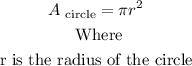
The radius is half of the diameter. Then, we have:

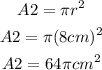
Calculating the area of the paper that remains
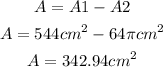
Answer
The area of the paper that remains rounding the nearest hundredth is 342.94 cm².