Question

- S1 - CR

ULIV viru
ignment: Reflect on the Lab
Active
Comparing Densities
two balls have the same volume, but ball A has twice as much mass as ball B, which one will have the greater
ensity?
ball C is 3 times the volume of ball D and ball D has 1/3 the mass of ball C, which has the greater density?
two balls have the same mass, but ball P is twice as large as ball Q, which one will have the greater density?
ball X is twice as big as ball Y and weighs only half as much as ball Y, then which one will have the greater
ensity?

Answer 1

Part C.

Given:

Mass of ball P, Mp = mass of ball Q, MQ

Volume of P, Vp = 2 times volume of ball Q, 2VQ

Let's determine the ball with the greater density.

Apply the formula:

`\rho=(m)/(v)`

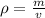
Now, for densities of both balls, we have:

`\begin{gathered} \rho_p=(m_p)/(v_p)=\frac{m_{}}{2v_Q} \\ \\ \rho_Q=(m)/(v_Q) \end{gathered}`

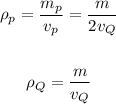
Now, divide density of P by density of Q:

`\begin{gathered} (\rho_P)/(\rho_Q)=((m)/(2v_Q))/((m)/(v_Q)) \\ \\ =(m)/(2v_Q)*(v_Q)/(m) \\ \\ =(1)/(2) \end{gathered}`

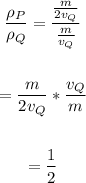
Therefore, the density of ball P is 1/2 the density of the density of ball Q.

Hence, ball Q will have a greater density.

• (d). ,Given:

Volume of ball X = 2 * volume of ball Y

Mass of X = 1/2 * mass of ball Y.

We have:

`\begin{gathered} \rho_X=((1)/(2)m_Y)/(2v_Y) \\ \\ \rho_Y=(m_Y)/(v_Y) \end{gathered}`

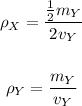
Divide density of ball X by that of ball Y:

`\begin{gathered} (\rho_X)/(\rho_Y)=(((1)/(2)m_Y)/(2v_Y))/((m_Y)/(v_Y)) \\ \\ =((1)/(2)m_Y)/(2v_Y)*(v_Y)/(m_Y) \\ \\ =(1)/(2)*(1)/(2) \\ \\ =(1)/(4) \end{gathered}`

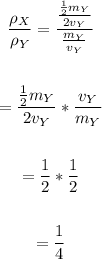
Therefore, the density of ball X is 1/4 the density of ball Y.

Hence, ball Y will have the greater density.

ANSWER:

(c). Ball Q has the greater density

(d). Ball Y has the greater density