Part C.
Given:
Mass of ball P, Mp = mass of ball Q, MQ
Volume of P, Vp = 2 times volume of ball Q, 2VQ
Let's determine the ball with the greater density.
Apply the formula:

Now, for densities of both balls, we have:
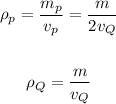
Now, divide density of P by density of Q:
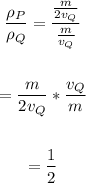
Therefore, the density of ball P is 1/2 the density of the density of ball Q.
Hence, ball Q will have a greater density.
• (d). ,Given:
Volume of ball X = 2 * volume of ball Y
Mass of X = 1/2 * mass of ball Y.
We have:
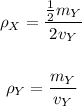
Divide density of ball X by that of ball Y:
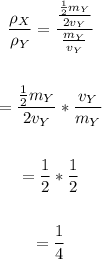
Therefore, the density of ball X is 1/4 the density of ball Y.
Hence, ball Y will have the greater density.
ANSWER:
(c). Ball Q has the greater density
(d). Ball Y has the greater density