Question

Find the length of each side of the triangle determined by the three points and state whether the triangle is an isosceles triangle, a right triangle, neither of these, or both. (An isosceles triangle is one in which at least two of the sides are of equal length.) P1 = (-4,-1), P2 = (0,9), P3 = (3,2)

Answer 1

Use the next formula to find the distance between two points:

`\begin{gathered} d=√((x_2-x_1)^2+(y_2-y_1)^2) \\ \end{gathered}`

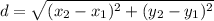
Sides of the triangle have the next lengths:

P1 to P2: (-4,-1) to (0,9)

`\begin{gathered} P1P2=√((0-(-4))^2+(9-(-1))^2) \\ \\ P1P2=√(4^2+10^2) \\ \\ P1P2=√(16+100) \\ \\ P1P2=√(116) \end{gathered}`

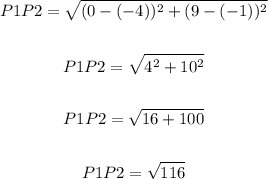
P2 to P3: (0,9) to (3,2)

`\begin{gathered} P2P3=√((3-0)^2+(2-9)^2) \\ \\ P2P3=√(3^2+(-7)^2) \\ \\ P2P3=√(9+49) \\ \\ P2P3=√(58) \end{gathered}`

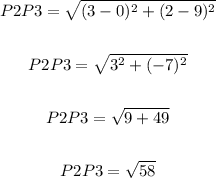
P3 to P1: (3,2) to (-4,-1)

`\begin{gathered} P3P1=√((-4-3)^2+(-1-2)^2) \\ \\ P3P1=\sqrt{(-7)\placeholder{⬚}^2+(-3)\placeholder{⬚}^2} \\ \\ P3P1=√(49+9) \\ \\ P3P1=√(58) \end{gathered}`

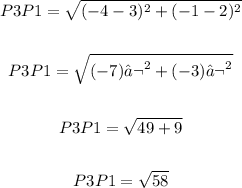
As the length of two sides of the triangle is the same it is a isosceles triangle.

To prove if it is a right triangle use the pythagorean theorem:

The greatest side needs to be the hypotenuse

`\begin{gathered} hyp^2=Leg1^2+Leg2^2 \\ \\ (√(116))\placeholder{⬚}^2=(√(58))\placeholder{⬚}^2+(√(58))\placeholder{⬚}^2 \\ \\ 116=58+58 \\ \\ 116=116 \end{gathered}`

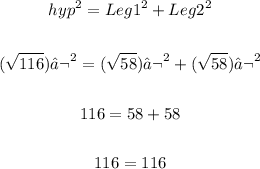
The given triangle makes true the pythagorean theorem, it is a right triangle.

Then, the given triangle has two equal sides and makes true the pythagorean theorem: it is a isosceles right triangle