Use the next formula to find the distance between two points:

Sides of the triangle have the next lengths:
P1 to P2: (-4,-1) to (0,9)
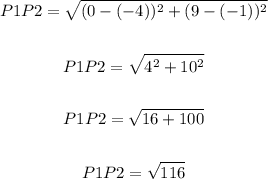
P2 to P3: (0,9) to (3,2)

P3 to P1: (3,2) to (-4,-1)
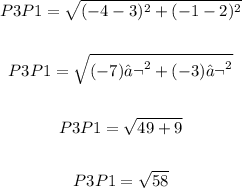
As the length of two sides of the triangle is the same it is a isosceles triangle.
To prove if it is a right triangle use the pythagorean theorem:
The greatest side needs to be the hypotenuse
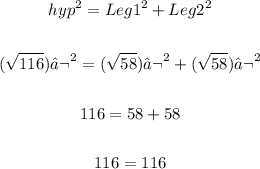
The given triangle makes true the pythagorean theorem, it is a right triangle.
Then, the given triangle has two equal sides and makes true the pythagorean theorem: it is a isosceles right triangle