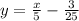Answer:
Writing the given equation in slope-intercept form we have;
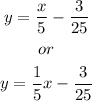
Step-by-step explanation:
Given the linear equation;
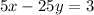
We want to turn the given linear equation to slope-intercept form.
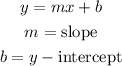
To do that, let us make y the subject of formula;
subtract 5x from both sides;
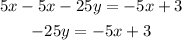
divide both sides by -25 (the coefficient of y);
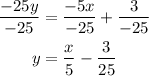
Therefore, writing the given equation in slope-intercept form we have;