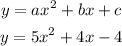We have been given 3 points on the quadratic function as
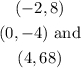
The quadratic equation would take the form

We now start with point (-2, 8) and we substitute the value of x as shown below;
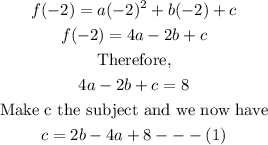
We now go on to point (0, -4);
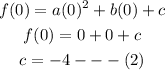
We now substitute for the value of c into equation (1)
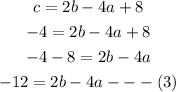
We now go on to the third point which is (4, 68)
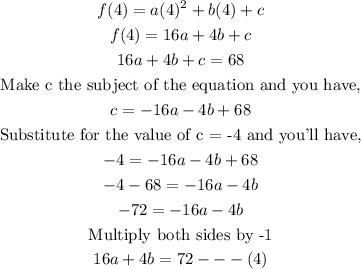
With equations (3) and (4) we can now determine the value of a and b as follows;

We can now substitute the value of b into equation (3)
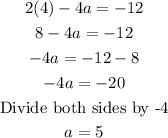
With the values of a = 5, b = 4 and c = -4, we now have