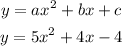Question

Fit a quadratic function to these three points: (-2,8),(0,-4)and (4,68) A. Y=-2x^2+2x-4B. Y=-4x^2-2x-4C. y=-2x^2-2x-4D. Y=4x^2+2x-4

Answer 1

We have been given 3 points on the quadratic function as

`\begin{gathered} (-2,8) \\ (0,-4)\text{ and} \\ (4,68) \end{gathered}`

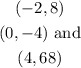
The quadratic equation would take the form

`f(x)=ax^2+bx+c`

We now start with point (-2, 8) and we substitute the value of x as shown below;

`\begin{gathered} f(-2)=a(-2)^2+b(-2)+c \\ f(-2)=4a-2b+c \\ \text{Therefore,} \\ 4a-2b+c=8 \\ \text{Make c the subject and we now have} \\ c=2b-4a+8---(1) \end{gathered}`

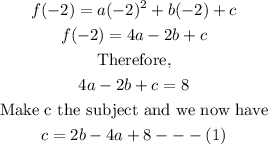
We now go on to point (0, -4);

`\begin{gathered} f(0)=a(0)^2+b(0)+c \\ f(0)=0+0+c \\ c=-4---(2) \end{gathered}`

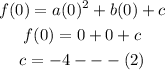
We now substitute for the value of c into equation (1)

`\begin{gathered} c=2b-4a+8 \\ -4=2b-4a+8 \\ -4-8=2b-4a \\ -12=2b-4a---(3) \end{gathered}`

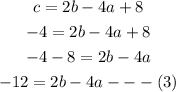
We now go on to the third point which is (4, 68)

`\begin{gathered} f(4)=a(4)^2+b(4)+c \\ f(4)=16a+4b+c \\ 16a+4b+c=68 \\ \text{Make c the subject of the equation and you have,} \\ c=-16a-4b+68 \\ \text{Substitute for the value of c = -4 and you'll have,} \\ -4=-16a-4b+68 \\ -4-68=-16a-4b \\ -72=-16a-4b \\ \text{Multiply both sides by -1} \\ 16a+4b=72---(4) \end{gathered}`

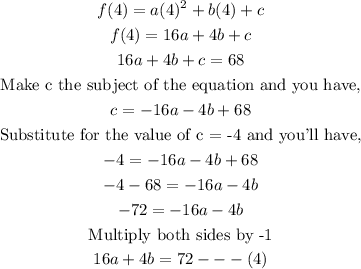
With equations (3) and (4) we can now determine the value of a and b as follows;

`\begin{gathered} 2b-4a=-12---(3) \\ 16a+4b=72---(4) \\ \text{Multiply (3) by 4 and multiply (4) by }2 \\ 8b-16a=-48---(5) \\ 32a+8b=144---(6) \\ \text{ Subtract (6) from (5)} \\ -16b-32b=-48-144 \\ -48b=-192 \\ \text{Divide both sides by -48} \\ b=4 \end{gathered}`

We can now substitute the value of b into equation (3)

`\begin{gathered} 2(4)-4a=-12 \\ 8-4a=-12 \\ -4a=-12-8 \\ -4a=-20 \\ \text{Divide both sides by -4} \\ a=5 \end{gathered}`

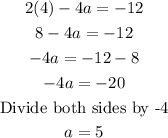
With the values of a = 5, b = 4 and c = -4, we now have

`\begin{gathered} y=ax^2+bx+c \\ y=5x^2+4x-4 \end{gathered}`