We have two different plans
x is the number of minutes
y= total cost in dollars
Part A)
Plan 1
y=0.20x
Plan 2
y=0.09x+49.95
Part B
In order that the second plan will be preferable, is when the plan 2 is cheaper so we will have the next inequality
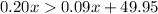
Then we need to solve the inequality
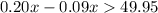

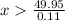
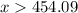
The nearest greater inter is 455
Therefore the minimum number of minutes you would have to use in a month in order for the second plan to be preferable is 455 minutes