Question

3. Triangle ABC and triangle A'B'C' are shown below. Triangles NOT to scale.BB1512Why is it certain that triangle A'B'C' is a dilation of triangle ABC?A. Because the areas of the triangles are equal to each other.B. Because triangle ABC and triangle A'B'C' are both triangles.C. Because triangle A'B'C' is a y-axis reflection of triangle ABC.D. Because the side lengths are proportional.

Answer 1

D. Because the side lengths are proportional.

Step-by-step explanation:

Given the attached image;

Triangle ABC and Triangle A'B'C'

Trangle A'B'C' can only be a dilation of Triangle ABC because the side length are proportional.

Dilation of a triangle produces a similar triangle with side length proportional.

`(AB)/(A^(\prime)B^(\prime))=(BC)/(B^(\prime)C^(\prime))=(AC)/(A^(\prime)C^(\prime))`

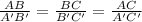
from the given values;

`\begin{gathered} (AB)/(A^(\prime)B^(\prime))=(4)/(12)=(1)/(3) \\ (BC)/(B^(\prime)C^(\prime))=(5)/(15)=(1)/(3) \\ (AC)/(A^(\prime)C^(\prime))=(3)/(9)=(1)/(3) \end{gathered}`

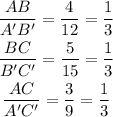
Therefore, the side lengths are proportional.