Answer:
D. Because the side lengths are proportional.
Step-by-step explanation:
Given the attached image;
Triangle ABC and Triangle A'B'C'
Trangle A'B'C' can only be a dilation of Triangle ABC because the side length are proportional.
Dilation of a triangle produces a similar triangle with side length proportional.
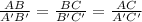
from the given values;
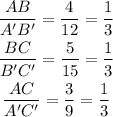
Therefore, the side lengths are proportional.