first at all, we need to remember the general equation of the line:

Now, we solve the given equation to y, like this:
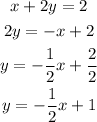
Fron that equation, we conclude that the slope is -1/2
Later, we need to remember that two lines are perpendiculars when the product of its slopes is -1. It means:
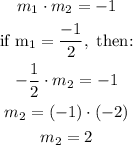
Finally, the slope of the line perpendicular to the line whose equation is x+2y=2 is 2.