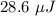Given:
The charge on the Y-axis is,

The initial position of the charge is,
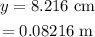
The final position of the charge is,
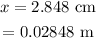
The charge at the origin is,
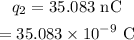
To find:
The work to move the charge
Step-by-step explanation:
The potential at the first point is,
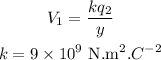
The potential at the final point is,
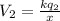
The work in this process is,

Hence, the work is,