Question

In the diagram, triangle ABC is isosceles. AB = AC, CB = 15 cm and angle ACB is 23°.

Answer 1

Since the given triangle is isosceles then the base angles are congruent. This means that angle CBA=BCA=25 degrees, that is,

Since interior angles of any triangle add up to 180 degrees, we get

`m\angle CAB+23+23=180`

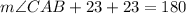
which gives

`m\angle CAB+46=180`

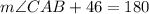
By substracting 46 to both sides, we obtain

`m\angle CAB=134`

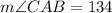
Therefore, the size of angle CAB is 134 degrees