Question

Where is system of equations to describe the situation below so I’m using substituttion And fill in the blanks

Answer 1

Let x be the number of hours spent typing by each student.

Since Mitchell can type at a speed of 3 pages per hour, and has already typed 9 pages, the expression that would model Mitchell's situation is:

`3x+9`

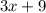
Similarly, Roxanne can type at a speed of 2 pages per hour, and has already typed 12 pages, the expression that would model Roxanne's situation is:

`2x+12`

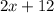
Now, we know that after some time both will have the exact same page count. Let's call this number y. This way, we'll have two equations that describe a system of equations:

`\begin{cases}y=3x+9 \\ y=2x+12\end{cases}`

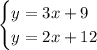
We'll solve it by substitution, so we'll solve the first equation for x, substitute in the second equation and then find the value of y, as following:

`\begin{gathered} y=3x+9\rightarrow y-9=3x\rightarrow(1)/(3)y-3=x \\ \\ y=2x+12 \\ \\ \rightarrow y=2((1)/(3)y-3)+12\rightarrow y=(2)/(3)y-6+12\rightarrow y-(2)/(3)y=6 \\ \\ \rightarrow(1)/(3)y=6\rightarrow y=18 \\ \end{gathered}`

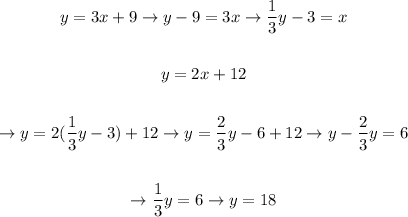
This way, we can conlcude that:

`y=18`

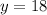
Since we've calculated an expression for x in terms of y , we just have to plug in this value in it to find the value of x:

`\begin{gathered} (1)/(3)y-3=x \\ \\ \rightarrow(1)/(3)(18)-3=x \\ \\ \rightarrow3=x \end{gathered}`

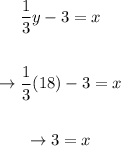
Therefore, the solution to our system is:

`\begin{gathered} x=3 \\ y=18 \end{gathered}`

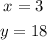
This way, we can conclude that: