Let x be the number of hours spent typing by each student.
Since Mitchell can type at a speed of 3 pages per hour, and has already typed 9 pages, the expression that would model Mitchell's situation is:
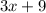
Similarly, Roxanne can type at a speed of 2 pages per hour, and has already typed 12 pages, the expression that would model Roxanne's situation is:
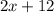
Now, we know that after some time both will have the exact same page count. Let's call this number y. This way, we'll have two equations that describe a system of equations:
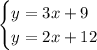
We'll solve it by substitution, so we'll solve the first equation for x, substitute in the second equation and then find the value of y, as following:
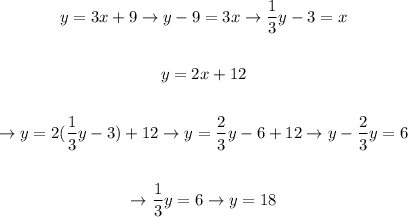
This way, we can conlcude that:
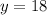
Since we've calculated an expression for x in terms of y , we just have to plug in this value in it to find the value of x:
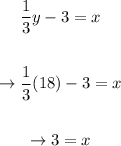
Therefore, the solution to our system is:
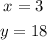
This way, we can conclude that: