Question

Determine the doubling time for each situation listed belowb. A bank account is growing by 2.7% each year compounded annually

Answer 1

26 years

Step-by-step explanation:

The amount at the end of t years can be calculated as:

`A=P(1+r)^t`

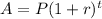
Where P is the principal and r is the interest rate.

If we want to find the doubling time, we need to replace A by 2P and solve for t, so we get:

`\begin{gathered} 2P=P(1+0.027)^t \\ (2P)/(P)=(P(1+0.027)^t)/(P) \\ 2=(1+0.027)^t \end{gathered}`
`\begin{gathered} 2=1.027^t \\ \log 2=t\log 1.027 \\ (\log 2)/(\log 1.027)=t \\ 26.01=t \end{gathered}`

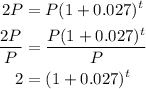
Therefore, the doubling time for this situation is approximately 26 years.