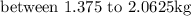Question

Jake is putting up a new show

Answer 1

Given:

`\begin{gathered} \text{lenght of each piece of wood = 3}(1)/(5)\text{ = 3.2 m} \\ Number\text{ of pieces of the same length = 8} \end{gathered}`

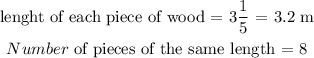
First question: An equation that shows how to find the total length

`\text{Total length = length of each piece of wood }*\text{ number of pieces}`

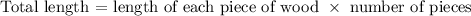
By substituting the given dimensions to find the actual measurement:

`\begin{gathered} \text{Total length = (3.2 }*\text{ 8) meters} \\ =\text{ 25.6 meters} \end{gathered}`
`\text{Jack measures the total length as 24}(1)/(5)\text{ meters or 24.2 m}`

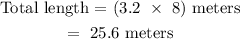
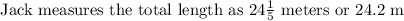
Is he correct?

The answer is NO

Why?

This is because Jack's measurement is not the same as the actual measurement

Given:

`\begin{gathered} 1\text{ box of nails has a mass of 2}(3)/(4)\text{ kg or 2.75kg} \\ He\text{ used betw}een\text{ }(1)/(2)\text{ to }(3)/(4)\text{ of the nails} \end{gathered}`

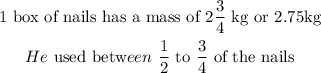
We are to find the kg of nails he used

Let us represent the total number of nails in the box as T

`It\text{ implies that Jack used betw}een\text{ }(1)/(2)T\text{ to }(3)/(4)T\text{ nails}`

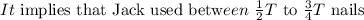
To obtain the kg of nails he used, we used the analogy:

`\begin{gathered} \text{If T nails weigh 2.75kg, } \\ \text{then }(1)/(2)T\text{ nails would weigh 1.375kg and } \\ (3)/(4)T\text{ nails would weigh 2.0625kg} \end{gathered}`

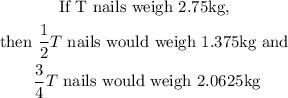
Hence, the kg of nails Jack used is :

`\text{between 1.375 to 2.0625kg}`