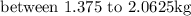Given:
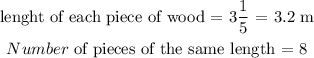
First question: An equation that shows how to find the total length
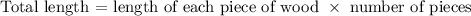
By substituting the given dimensions to find the actual measurement:
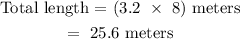
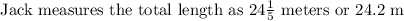
Is he correct?
The answer is NO
Why?
This is because Jack's measurement is not the same as the actual measurement
Given:
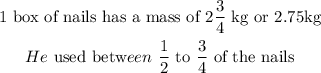
We are to find the kg of nails he used
Let us represent the total number of nails in the box as T

To obtain the kg of nails he used, we used the analogy:
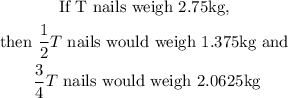
Hence, the kg of nails Jack used is :