Given:
The number of letters in the account number is, n(A) = 3.
The number of digits in the account number is, n(D) = 5.
The objective is to find the number of possible account numbers with repetitions.
Step-by-step explanation:
The total number of letters is, N(A)=26.
The total number of digits is, N(D)=13.
The formula to find the number of possible numbers are,

To find the number of possibilities:
Substitute the obtained values in equation (1).
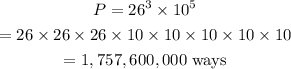
Hence, there are 1,757,600,000 ways