Question

i have 8 questions i need help withTrucks in a delivery fleet travel a mean of 100 miles per day with a standard deviation of 36 miles per day. The mileage per day is distributed normally. Find the probability that a truck drives between 60 and 157 miles in a day. Round your answer to four decimal places.

Answer 1

The formula for the z-score is

From the problem, we have :

mean = 100

standard deviation = 36

We are looking for theprobability of the z-scores between 60 and 157

Using the formula above :

`\begin{gathered} z=(60-100)/(36)=-1.11 \\ z=(157-100)/(36)=1.58 \end{gathered}`

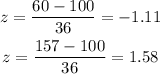
Using the normal distribution table. Find P(-1.11 < z < 1.58)

Note that :

P(-1.11 < z < 1.58) = P(z < 1.58) - P (z < -1.11)

P(z < 1.58) = 0.9429

P(z < -1.11) = 0.1335

Solve the value of P(-1.11 < z < 1.58) :

0.9429 - 0.1335 = 0.8094

The answer is 0.8094