The formula for the z-score is
![z=\frac{x-\operatorname{mean}}{\text{standard deviation}}]()
From the problem, we have :
mean = 100
standard deviation = 36
We are looking for theprobability of the z-scores between 60 and 157
Using the formula above :
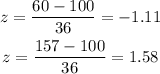
Using the normal distribution table. Find P(-1.11 < z < 1.58)
Note that :
P(-1.11 < z < 1.58) = P(z < 1.58) - P (z < -1.11)
P(z < 1.58) = 0.9429
P(z < -1.11) = 0.1335
Solve the value of P(-1.11 < z < 1.58) :
0.9429 - 0.1335 = 0.8094
The answer is 0.8094