Question

The population of the world in 1987 was 5 billion and the annual growth rate was estimated at 1.3% per year. Assuming that the world population follows an exponential growth model, find the projected world population in 2020. Round your answer to 1 decimal place.

Answer 1

Given

Population of the world in 1987 = 5 billion

Annual growth rate = 1.3% per year

Required: The projected population in 2020

The exponential population growth formula is defined as:

`\begin{gathered} P\text{ = P}_0e^(rt) \\ Where\text{ P}_0\text{ is the initial population} \\ r\text{ is the \% growth rate} \\ and\text{ t is the time in years} \end{gathered}`

Substituting the given values:

`P(t)\text{ = 5000000000e}^(0.013t)`

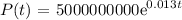
After 2020, t = 33 years

Hence, the population after 33 years is:

`\begin{gathered} P(t=13)\text{ = 5000000000 }*\text{ e}^(0.013*33) \\ =\text{ 7678605171.987} \\ =\text{ 7678605172.0} \end{gathered}`

Hence, the estimated population of the world in 2020 is 7678605172.0