Question

f(x)=2log(-1/2x-1)+11) complete a table of values for the key points and determine the translated key points 2) write a mapping formula 3) sketch the starting function and the new graph

Answer 1

`f(x)=2\log (-(1)/(2)x-1)+1`

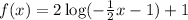
Let's complete the table starting from the parent function y = log x. Plug in the given value of x to the parent function.

For example, at x = 1/10, y = log 1/10 = -1.

At x = 1, y = log 1 = 0.

At x = 10, y = log 10 = 1

At x = 32, y = log 32 = 1.505.

Let's move on to the other table for the given function above.

As we can see in the given function, the log function has been subtracted by 1. Hence, we can infer that there is a reflection over the y-axis between the parent function and the new function.

With this, we will assume the value of y that we got in the first table and solve for the value of x for the second table.

Plug in y = -1 in the new function and solve for x.

`\begin{gathered} y=2\log (-(1)/(2)x-1)+1 \\ -1=2\log (-(1)/(2)x-1)+1 \\ \text{Subtract 1 on both sides.} \\ -2=2\log (-(1)/(2)x-1) \\ \text{Divide 2 on both sides.} \\ -1=\log (-(1)/(2)x-1) \\ \text{Convert to exponential form.} \\ -(1)/(2)x-1=10^(-1) \\ -(1)/(2)x-1=(1)/(10) \\ \text{Add 1 on both sides.} \\ -(1)/(2)x=1.1 \\ \text{Divide -0.5 on both sides.} \\ x=-2.2 \end{gathered}`

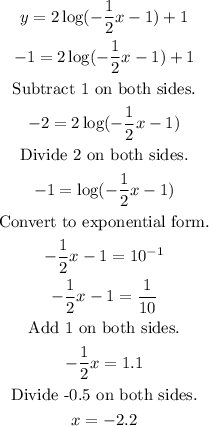
Hence, at y = -1, x = -2.2.

Let's move on to the next keypoint at y = 0.

`\begin{gathered} 0=2\log (-(1)/(2)x-1)+1 \\ -1=2\log (-(1)/(2)x-1) \\ -(1)/(2)=\log (-(1)/(2)x-1) \\ -(1)/(2)x-1=10^{-(1)/(2)} \\ -(1)/(2)x-1=0.316227766 \\ -(1)/(2)x=1.316227766 \\ x=-2.632 \end{gathered}`

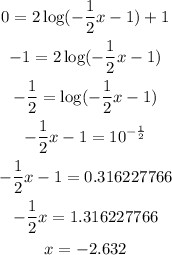
At y = 0, x = -2.632.

Moving on to the next keypoint at y = 1.

`\begin{gathered} 1=2\log (-(1)/(2)x-1)+1 \\ 0=2\log (-(1)/(2)x-1) \\ 0=\log (-(1)/(2)x-1) \\ (-(1)/(2)x-1)=10^0 \\ -(1)/(2)x-1=1 \\ -(1)/(2)x=2 \\ x=-4 \end{gathered}`

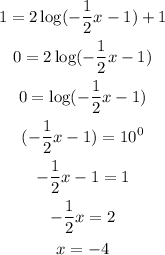
At y = 1, x = -4.

Last keypoint at y = 1.505.

`\begin{gathered} 1.505=2\log (-(1)/(2)x-1)+1 \\ 0.505=2\log (-(1)/(2)x-1) \\ 0.2525=\log (-(1)/(2)x-1) \\ -(1)/(2)x-1=10^(0.2525) \\ -(1)/(2)x-1=1.79 \\ -(1)/(2)x=2.79 \\ x=-5.58 \end{gathered}`

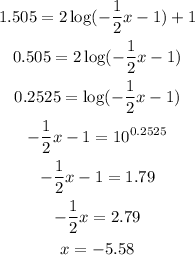
At y = 1.505, x = -5.58.

Putting this on the table, we have:

The graph of the two function is shown below:

The purple one is the graph of the parent function. The green one is the new function.