Question

A fish swims 12 miles upstream in 4 hours. The return trip takes only 3 hours. Find the rate of the current. A. 0.5 mph B. 1 mph C 4 mph D. 2 mph E. 3 mph

Answer 1

Let's use the variable x to define the fish speed, and the variable y to define the current speed.

If the fish swims 12 miles upstream in 4 hours, the relative speed in this case is 12/4 = 3, and it is the fish speed minus the current speed, so we have:

`x-y=3`

Then, the return trip takes only 3 hours, so the relative speed is 12/3 = 4, and it's the sum of the fish and current speeds:

`x+y=4`

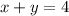
Adding both equations, we have:

`\begin{gathered} x-y+x+y=3+4 \\ 2x=7 \\ x=3.5 \end{gathered}`

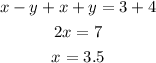
Now, calculating y, we have:

`\begin{gathered} x+y=4 \\ 3.5+y=4 \\ y=4-3.5 \\ y=0.5 \end{gathered}`

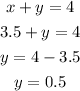
So the rate of the current is 0.5 mph, therefore the correct option is A.