ANSWER
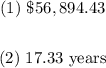
Step-by-step explanation
(1) The formula for the amount for a continuously compounded interest is given by:
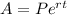
where P = principal (initial amount) = $30000
r = interest rate = 4% = 0.04
t = number of years
To find the amount he has after 16 years, find the value of A when t is 16:
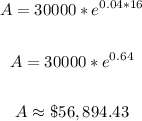
That is the amount in the account after 16 years.
(2) To find how long it takes for the money to double, we have to find t when A is $60000:
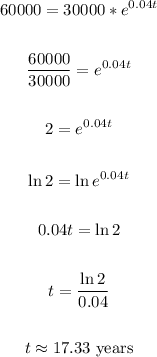
That is the time that it will take for the money to double.