Question

Mike deposited $30000 in a saving account in which interest is compounded continuously. The annual rate of interest is 4%.(1) How much does he have in this account after 16 years? (Round your answer to two decimal places.) dollars (2) How long does it take for his money to double? (Round your answer to two decimal places.) years

Answer 1

`\begin{gathered} (1)\text{ }\$56,894.43 \\ \\ (2)\text{ }17.33\text{ years} \end{gathered}`

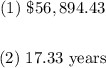
Step-by-step explanation

(1) The formula for the amount for a continuously compounded interest is given by:

`A=Pe^(rt)`

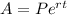
where P = principal (initial amount) = $30000

r = interest rate = 4% = 0.04

t = number of years

To find the amount he has after 16 years, find the value of A when t is 16:

`\begin{gathered} A=30000*e^(0.04*16) \\ \\ A=30000*e^(0.64) \\ \\ A\approx\$56,894.43 \end{gathered}`

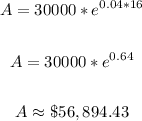
That is the amount in the account after 16 years.

(2) To find how long it takes for the money to double, we have to find t when A is $60000:

`\begin{gathered} 60000=30000*e^(0.04t) \\ \\ (60000)/(30000)=e^(0.04t) \\ \\ 2=e^(0.04t) \\ \\ \ln2=\ln e^(0.04t) \\ \\ 0.04t=\ln2 \\ \\ t=(\ln2)/(0.04) \\ \\ t\approx17.33\text{ years} \end{gathered}`

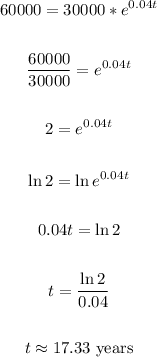
That is the time that it will take for the money to double.