Axis of symmetry
In a quadratic function, the axis of symmetry is given by the vertical line that passes through its vertex. Finding the vertex is one of the possible ways to find this axis. Another way is possible if the function has one or two zeros. In the first case the axis of symmetry intercepts the x-axis at the x-value of the zero of the function. In the second case, the axis of symmetry intercepts the x-axis at the midpoint between zeros. Remember that for a quadratic function like g(x)=ax²+bx+c its zeros are given by:
![x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/rxvf73usjbbwyik14knxdemoz21vfz2ufc.png)
Axis of symmetry of f(x)
Here we have the following function:

Let's find its roots using the formula above. We have a=1, b=6 and c=8 so its zeros are given by:
![\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}=\frac{-6\pm\sqrt[]{6^2-4\cdot1\cdot8}}{2\cdot1}=\frac{-6\pm\sqrt[]{36-32}}{2} \\ x=\frac{-6\pm\sqrt[]{36-32}}{2}=\frac{-6\pm\sqrt[]{4}}{2}=(-6\pm2)/(2) \\ x=-2\text{ and }x=-4 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/bk32yv3vwxoeuh8pbkzh88kvzzbmzu9ctq.png)
So the x-values of the zeros of f(x) are x=-2 and x=-4. Then the midpoint between them is given by their sum divided by 2:
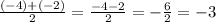
So the equation of the axis of symmetry is x=-3. And the answer is option C.