The given equation is:
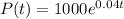
It is required to find when the population will exceed 1455.
To do this, substitute the given population and solve the resulting equation for t:
Substitute P(t)=1455 into the equation:
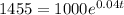
Solve the equation for t:
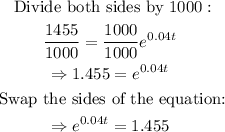
Take the natural logarithm of both sides:
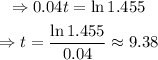
Hence, the population will exceed 1455 when t is about 9.38.
The population will exceed 1455 when t is about 9.38.