Question

Line I has the equation y=x+5. Find the distance between I and the point V(-6,-4). Round your answer to the nearest tenth.

Answer 1

The distance between the point and the line is 2.1 units

Here, we want to find the distance between the given line and the given point

Firstly, let us write the line in the standard form

That is;

`y\text{ = mx + b}`

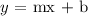
m represents the slope, which is the coefficient of x

The coefficient of x here is 1, and that means the slope of the line is 1

Now, we need the slope of a line perpendicular to this line

A line that is perpendicular to this line will have a slope that is the negative reciprocal of the slope of the given line

This means that the slope of the new line is;

`\begin{gathered} m_1* m_2\text{ = -1} \\ m_2\text{ = }(-1)/(1) \\ m_2\text{ = -1} \end{gathered}`

The slope of the line perpendicular to the given line is -1

Using this slope, we need to get the value of the y-intercept of the second line

That can be obtained by substituting the coordiates of the point given

We have this as;

`\begin{gathered} \text{for second line (perpendicular line);} \\ y\text{ = -x + b} \\ -4\text{ = -1(-6) + b} \\ -4\text{ = 6+b} \\ b\text{ = -4-6} \\ b\text{ = -10} \end{gathered}`

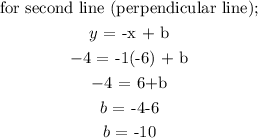
Now, we need to find the point of intersection of the two lines; we can get this by solving both equations simultaneously

The second equation line is given as;

`y\text{ = -x -10}`

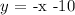
Solving it simultaenously, let us equate the two y;

`\begin{gathered} -x-10\text{ = x+5} \\ 2x\text{ = -5-10} \\ 2x\text{ = -15} \\ x\text{ = }(-15)/(2) \\ x\text{ = -7.5} \\ y\text{ = x+5 = -7.5+5 = -2.5} \end{gathered}`

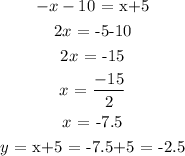
The point of intersection of the two perpendicular lines is (-7.5,-2.5)

We now proceed to find the distance between the given point and the point of intersection

That is the distance between (-6,-4) and (-7.5,-2.5)

We use the distance formula here;

`\begin{gathered} D\text{ = }\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ (x_1,y_1)\text{ = (-6,-4)} \\ (x_2,y_2)\text{ = (-7.5,-2.5)} \\ D\text{ = }\sqrt[]{(-7.5+6)^2+(-2.5+4)^2} \\ D\text{ = }\sqrt[]{2.25\text{ +2.25}} \\ D\text{ = }\sqrt[]{4.5} \\ D\text{ = 2.1} \end{gathered}`