Given: Ellie's height function
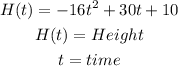
To Determine: The two times when the height was 15 feet
Solution
Given the quadratic formula below
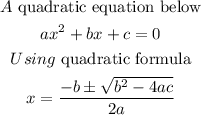
When height is 15 feet
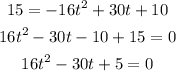
Using quadratic formula
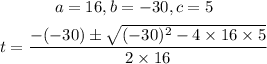
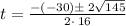
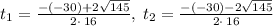
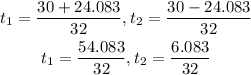
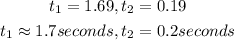
Hence, the two times Ellies height was 25 feet is 1.7 seconds and 0.2 seconds