We have the next system of equations
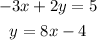
First, we need to substitute the value of y of the second equation in the first equation.
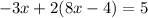
Then we simplify the expression
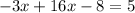
then we sum like terms
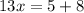
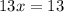
then we isolate the x
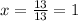
the value of x is 1.
Then to know the value of y we will substitute the value of x in the second equation
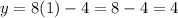
the value of y is 4.
The solution of the system of equations is x=1, y=4 in point notation (1,4) this system only has one solution.