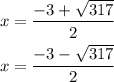Question

Use the following function to answer parts a through C. Part b says Use synthetic division to test several possible rational zeros in order to identify one actual zeroOne rational zero of the given function is ____Part c. Use the zero from part b to find all the zeros of the polynomial function. The zero of the function are ____________

Answer 1

According to the Rational Zeros Theorem, a polynomial with integer coefficients has a rational root in the form p/q, where p is a factor of the constant term and q is a factor of the leading coefficient.

We have the polynomial:

`x^3+4x^2-74x-77`

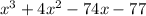
a.

The factors of the constant term are:

And the factors of the leading coefficient are -1 and +1.

Thus, the possible zeros are (comma-separated):

-1, +1, -7, +7, -11, +11, -77, +77

b. Now we use synthetic division to find the rational root from the list above.

Let's start with x = +1:

1 4 -74 -77

+ 1 +1 5 -69

--------------------------------

1 5 -69 -146

Since the last result is not zero, x = 1 is not a root of the polynomial.

Let's try x = -1:

1 4 -74 -77

- 1 -1 - 3 +77

--------------------------------

1 3 -77 0

The last result is 0 thus, x = -1 is a rational zero of the function.

One rational zero of the given function is -1

c.

The zero we have found in part b helps us to find the other two zeros. The three coefficients remaining in the last row are the coefficients of the quadratic polynomial a = 1, b = 3, c = -77 which can be solved by using the formula:

`$$x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}$$`

Substituting:

`\begin{gathered} x=(-3\pm√(3^2-4*1*\left(-77)\right?))/(2*1) \\ x=(-3\pm√(9+308))/(2)=(-3\pm√(317))/(2) \end{gathered}`

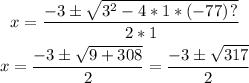
We have two different zeros:

`\begin{gathered} x=(-3+√(317))/(2) \\ x=(-3-√(317))/(2) \end{gathered}`