Answer:
• Vertex: (5,-2)
,
• Points to the left of the vertex: (3,2) and (4,-1)
,
• Points to the right of the vertex: (7,2) and (6, -1)
Step-by-step explanation:
Given the equation of the parabola:

First, determine the vertex:
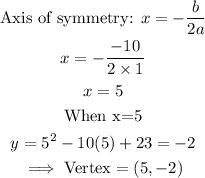
A table of values for the function is given below with the vertex identified:
Thus, we have the graph below:
• Vertex: (5,-2)
• Points to the left of the vertex: (3,2) and (4,-1)
,
• Points to the right of the vertex: (7,2) and (6, -1)