Question

Graph the parabola.y=x2 - 10x + 23Plot five points on the parabola: the vertex, two points to the left of the vertex, and two points to the right of the vertex. Then click onthe graph-a-function button.12-110х5?42-1010-

Answer 1

• Vertex: (5,-2)

,

• Points to the left of the vertex: (3,2) and (4,-1)

,

• Points to the right of the vertex: (7,2) and (6, -1)

Step-by-step explanation:

Given the equation of the parabola:

`y=x^2-10x+23`

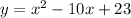
First, determine the vertex:

`\begin{gathered} \text{Axis of symmetry: }x=-(b)/(2a) \\ x=-(-10)/(2*1) \\ x=5 \\ \text{When x=5} \\ y=5^2-10(5)+23=-2 \\ \implies\text{Vertex}=(5,-2) \end{gathered}`

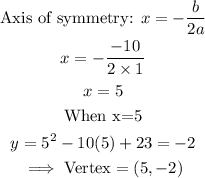
A table of values for the function is given below with the vertex identified:

Thus, we have the graph below:

• Vertex: (5,-2)

• Points to the left of the vertex: (3,2) and (4,-1)

,

• Points to the right of the vertex: (7,2) and (6, -1)