Question

2age 3:Find the vertex and the intercepts of the graph of the function.f (x) = (x + 2)2 – 9Do not enter any spaces in the answers.3The vertex isage 4:AEnter the x-intercepts as two points separated by a comma. Do not enter any spacds.A/ge 5:The y-intercept is the pointA/ge 6:Previous Page1Next PagePage 10 of 35Help ASAP no links

Answer 1

Vertex = (-2, - 9)

X- intercept: (-5, 0), (1, 0)

y-intercept: (0, -5)

Step-by-step explanation:

If we have a quadratic equation of the form

`y=(x-k)^2+h`

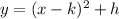
then the vertex is given by

`\text{vertex}=(k,h)`

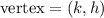
Now, in our case we have

`y=(x+2)^2-9`

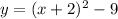
meaning k = -2 and h = - 9; therefore, the vertex is at

`vertex=(-2,9)`

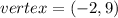
The intercepts of the parabola are the points where it intersects the x-axis. This happens when y = 0.

Putting in y = 0 in the equation for the parabola gives

`0=(x+2)^2-9`

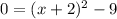
adding 9 to both sides gives

`(x+2)^2=9`

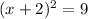
taking the square root of both sides gives

`\sqrt[]{(x+2)^2}=\sqrt[]{9}`

`x+2=\pm3`

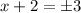
subtracting 2 from both sides gives

`x=\pm3-2`

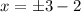
which gives us two solutions

`\begin{gathered} x=-3-2=-5 \\ x=3-2=1 \end{gathered}`

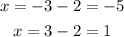
Hence, the x-intercepts of the parabola are at

`\begin{gathered} (-5,0) \\ (1,0) \end{gathered}`

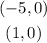
Now, we find the y-intercept.

The y-intercept is the point at which the parabola intersects the y-axis.

This happens when x = 0.

Putting in x = 0 in the equation for the parabola gives

`\begin{gathered} y=(x+2)^2-9 \\ y=(0+2)^2-9 \\ y=4-9 \\ \boxed{y=-5} \end{gathered}`

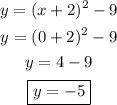
Hence, the y-intercept is at

`(0,-5)`

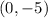
To summarize our results,

Vertex = (-2, - 9)

X- intercept: (-5, 0), (1, 0)

y-intercept: (0, -5)