Answer:
Vertex = (-2, - 9)
X- intercept: (-5, 0), (1, 0)
y-intercept: (0, -5)
Step-by-step explanation:
If we have a quadratic equation of the form
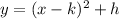
then the vertex is given by

Now, in our case we have
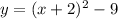
meaning k = -2 and h = - 9; therefore, the vertex is at
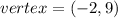
The intercepts of the parabola are the points where it intersects the x-axis. This happens when y = 0.
Putting in y = 0 in the equation for the parabola gives
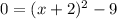
adding 9 to both sides gives
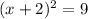
taking the square root of both sides gives
![\sqrt[]{(x+2)^2}=\sqrt[]{9}](https://img.qammunity.org/2023/formulas/mathematics/college/p5uvfzd9c0jiqmhukbw1tao65kji4zp86l.png)

subtracting 2 from both sides gives
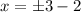
which gives us two solutions
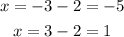
Hence, the x-intercepts of the parabola are at
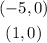
Now, we find the y-intercept.
The y-intercept is the point at which the parabola intersects the y-axis.
This happens when x = 0.
Putting in x = 0 in the equation for the parabola gives
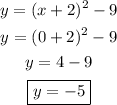
Hence, the y-intercept is at
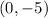
To summarize our results,
Vertex = (-2, - 9)
X- intercept: (-5, 0), (1, 0)
y-intercept: (0, -5)