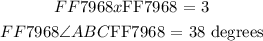Question

BD bisects ZABC. Solve for x and find m ZABC.mZABD = 9x - 8. mZCBD=6x + 1XmZABC=°Enter your answer in the answer box and then click Check Answer.All parts showing

Answer 1

We will use the angle properties to determine the constituent angles.

We are given that a line segment ( BD ) is an angle bisector of < ABC. We will go ahead and represent this piece of information graphically as follows:

We will define the following angle as follows:

`m\angle ABC\text{ = }\vartheta`

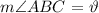
The angle bisector ( BD ) divides the angle into two equal halves as follows:

`m\angle ABD\text{ = m}\angle CBD\text{ = }(\angle ABC)/(2)=(\vartheta)/(2)`

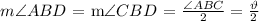
We are given expressions for both angles as follows:

`\begin{gathered} m\angle ABD\text{ = 9x - 8 } \\ m\angle CBD\text{ = 6x + 1} \end{gathered}`

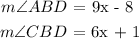
We know from the property of angle bisector that the two constituent angles are equal i.e:

`\begin{gathered} m\angle ABD\text{ = m}\angle CBD \\ 9x\text{ - 8 = 6x + 1} \\ 3x\text{ = 9} \\ \textcolor{#FF7968}{x}\text{\textcolor{#FF7968}{ = 3}} \end{gathered}`

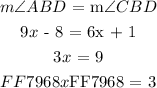
Now we can use the value of ( x ) calculated above and determine either of the constituent angles as follows:

`\begin{gathered} m\angle ABD\text{ = 9}\cdot(3)\text{ - 8 = 19 degrees} \\ m\angle CBD\text{ = 6}\cdot(3)\text{ + 1 = 19 degrees} \end{gathered}`

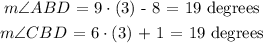
Then we can use the angle bisector property relation again to determine the angle ABC as follows:

`\begin{gathered} m\angle ABD\text{ = m}\angle CBD\text{ = }(\angle ABC)/(2) \\ 19\text{ degrees = }(\angle ABC)/(2) \\ \textcolor{#FF7968}{\angle ABC}\text{\textcolor{#FF7968}{ = 38 degrees}} \end{gathered}`

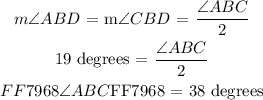
Answer:

`\begin{gathered} \textcolor{#FF7968}{x}\text{\textcolor{#FF7968}{ = 3}} \\ \textcolor{#FF7968}{\angle ABC}\text{\textcolor{#FF7968}{ = 38 degrees}} \end{gathered}`