We will use the angle properties to determine the constituent angles.
We are given that a line segment ( BD ) is an angle bisector of < ABC. We will go ahead and represent this piece of information graphically as follows:
We will define the following angle as follows:
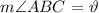
The angle bisector ( BD ) divides the angle into two equal halves as follows:
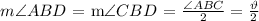
We are given expressions for both angles as follows:
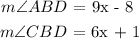
We know from the property of angle bisector that the two constituent angles are equal i.e:
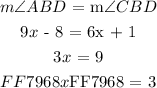
Now we can use the value of ( x ) calculated above and determine either of the constituent angles as follows:
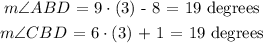
Then we can use the angle bisector property relation again to determine the angle ABC as follows:
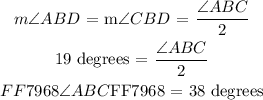
Answer:
