Question

I have a math question could I send you a picture of that to solve that for me

Answer 1

`\angle R=44^(\circ),\angle A=69^(\circ),\angle P=79^(\circ)`

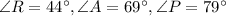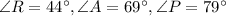
2) In these problems, let's make use of the Law of Cosines since in each triangle we have their legs and just want to know the measure of one angle.

a) Let's begin with that, bearing in mind the following formula:

`\begin{gathered} a^2=b^2+c^2-2bc\cdot\cos (A) \\ r^2=s^2+t^2-2st\cdot cos(R) \end{gathered}`

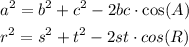
Note that the leg "r" is opposite to the angle (R):

`r^2=s^2+t^2-2st\cdot cos(R)`

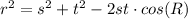
But note that we have a right triangle and we don't know the side "t". So, let's use the Pythagorean Theorem to find the missing side "t":

`\begin{gathered} a^2=b^2+c^2 \\ 10^2=8^2+c^2 \\ 100-64=c^2 \\ c=\sqrt[]{36} \\ c=6 \end{gathered}`

So now, let's get back to the Cosines Law:

`\begin{gathered} r^2=s^2+t^2-2st\cdot cos(R) \\ 8^2=10^2+6^2-2(10)(6)\cdot\cos (R) \\ 64=100+36-120\cos (R) \\ 64=136-120\cos (R) \\ 120\cos (R)=136-64 \\ (120\cos (R))/(120)=(72)/(120) \\ R=\cos ^(-1)((72)/(100)) \\ R=43.94\approx44^(\circ) \end{gathered}`

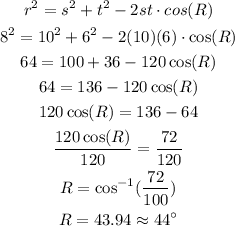
b) In this one, we can see the angle 38º and the missing angle "A". We can use the Law of the Sines to find that angle.

`\begin{gathered} (c)/(\sin(C))=(b)/(\sin (B)) \\ (55)/(\sin(38))=(85)/(\sin (B)) \\ 55\sin (B)=85\cdot\sin (38) \\ (55\sin (B))/(55)=(85\cdot\sin (38))/(55) \\ \sin (B)=0.95147 \\ B=\sin ^(-1)(0.95147) \\ B=72.5865\approx73^(\circ) \end{gathered}`

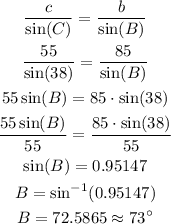
Now, that we know angle B, we can write out this equation since the sum of the interior angles is 180º

`\begin{gathered} \angle A+\angle B+\angle C=180^(\circ) \\ \angle A+73+38=180 \\ \angle A=180-(73+38) \\ \angle A=69^(\circ) \end{gathered}`

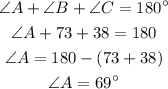
c) Finally, we can apply the Cosines Law for this triangle:

`\begin{gathered} p^2=q^2+r^2-2qr\cdot\cos (P)_{} \\ 2.5^2=1.7^2+2.2^2-2(1.7)(2.2)\cos (P) \\ 6.25=2.89+4.84-7.48\cos (P) \\ 6.25=7.73-7.48\cos (P) \\ 6.25-7.73=-7.48\cos (P) \\ -1.48=-7.48\cos (P) \\ P=\cos ^(-1)((1.48)/(7.48)) \\ P=78.58^(\circ)\approx79^(\circ) \end{gathered}`

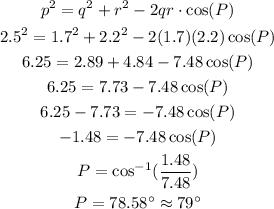
2) Thus the answer is:

`\angle R=44^(\circ),\angle A=69^(\circ),\angle P=79^(\circ)`