1 Answer

Danyal Imran · Answer 1 · 2023-03-26T13:58:01+0000

Answer:

He was supposed to cross multiply the equation in the original equation. Step 2 was a wrong expression

Explanations:

The given equation is:

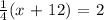
$(1)/(4)(x\text{ + 12) = 2}$

Cross multiply the equation, the equation becomes:

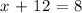
$x\text{ + 12 = 8}$

x = 8 - 12

x = -4

His mistake was in step 2, he did not properly expand the equation

The proper step was to cross multiply in step 2

Please log in or register to add a comment.